The mathematics behind smart contracts

Smart contracts are self-executing contracts with the terms of the agreement between buyer and seller being directly written into lines of code. They are digital agreements that are stored and executed on a blockchain network. They allow for the automatic and secure execution of the terms of a contract without the need for intermediaries. The mathematics behind smart contracts plays a crucial role in ensuring the security, immutability, and enforceability of these agreements.

Cryptographic techniques, such as hash functions and digital signatures, are used to secure and verify the execution of the contract. Logical gates and boolean algebra are used to encode the terms of the contract in a way that can be understood and processed by a computer. Other mathematical concepts and techniques, such as finite state machines and mathematical proof, may also be used in the design and analysis of smart contracts. These mathematical tools help to ensure that the contract will behave as intended and that the terms of the agreement are accurately enforced.

Logical gates are basic components of digital circuits that perform Boolean logic operations, such as AND, OR, and NOT. These operations can be used to create more complex logic circuits that encode the conditions and actions specified in a contract. For example, consider the following smart contract that specifies that if a payment is received, then the goods should be shipped:

[Payment received] AND [Goods not yet shipped] -> [Ship goods]

This logical relationship can be encoded using logical gates, as shown in the following diagram:

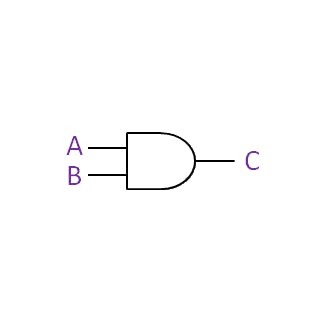
[Payment received] is represented by input A, [Goods not yet shipped] is represented by input B, and [Ship goods] is represented by output C. The AND gate in the middle performs the AND operation on inputs A and B, and the resulting output is C. If both inputs are 1 (true), then the output is also 1 (true). If either input is 0 (false), then the output is 0 (false).

Boolean algebra is a branch of algebra in which all values are either true or false (i.e., 1 or 0). It is used to simplify and manipulate logical expressions, which are combinations of logical variables and logical operators (e.g., AND, OR, NOT). For example, the following logical expression represents the same condition-action relationship as the logical circuit above:

C = A AND B

This expression can be read as "C is equal to A AND B," where C is the output, A is the input representing [Payment received], and B is the input representing [Goods not yet shipped].

Boolean algebra is used in the design and analysis of digital circuits, including smart contracts, as it allows complex logical relationships to be represented and manipulated in a concise and logical way.

In addition to logical gates and boolean algebra, smart contracts may also use other mathematical concepts and techniques, such as finite state machines and mathematical proof, to encode and verify the terms of the contract.

Finite state machines (FSMs) are a mathematical model used to represent and analyze the behavior of systems that can be in one of a finite number of states. In the context of smart contracts, FSMs can be used to encode the different states that a contract can be in and the transitions between those states. For example, a smart contract for a simple auction might have the following states and transitions:

● Initial state: the auction has not yet started

● Accepting bids state: the auction is open and bids are being accepted

● End of auction state: the auction has closed and the highest bidder has been determined

● Payment state: the highest bidder is required to make payment

● Delivery state: the seller is required to deliver the goods to the highest bidder

Each of these states can be represented by a node in the FSM, and the transitions between states can be represented by directed edges between the nodes. The FSM for this auction contract might look something like this:

[Initial state] <-- [Accepting bids state] <-- [End of auction state] --> [Payment state] --> [Delivery state]

FSMs can be used to model and analyze the behavior of smart contracts, as they allow the different states and transitions of the contract to be represented and analyzed in a precise and logical way.

Mathematical proof is another mathematical technique that can be used in the design and analysis of smart contracts. Proofs are used to rigorously demonstrate the correctness of a statement or claim. In the context of smart contracts, proofs can be used to illustrate the correctness of the logic encoded in the contract and to ensure that the contract will behave as intended. For example, a proof might be used to show that a contract will always transition from the initial state to the accepting bids state at the start of an auction and that it will only transition to the end of the auction state once the auction has closed.

Overall, the mathematics behind smart contracts includes the use of logical gates and boolean algebra to encode the terms of a contract in a way that can be understood and processed by a computer, as well as techniques such as finite state machines and mathematical proof to verify the correctness and behavior of the contract. Logical gates perform basic Boolean logic operations, such as AND, OR, and NOT, which can be used to create more complex logic circuits that encode the conditions and actions specified in a contract. Boolean algebra is a branch of algebra in which all values are either true or false, and it is used to simplify and manipulate logical expressions, which are combinations of logical variables and operators. Finite state machines are a mathematical model used to represent and analyze the behavior of systems that can be in one of a finite number of states, and they can be used to model and analyze the behavior of smart contracts. And the mathematical proof is a technique used to rigorously demonstrate the correctness of a statement or claim, and it can be used to verify the correctness of the logic encoded in a smart contract and to ensure that the contract will behave as intended.